Magnetômetro Vetorial
Pesquisador Responsável: Dr. Hans Marin Florez

Entre os sistemas que têm atraído a atenção para o desenvolvimento de sensores quânticos estão os vapores atômicos, que apresentam um amplo espectro de aplicações, entre elas, magnetometria, geração de luz comprimida, ressonância magnética, relógios atômicos, detecção de luz de Tera-Hertz e a busca de partículas de matéria escura [11-17]. A sua relativa facilidade de saturação ótica das transições atômicas permite a observação de efeitos de não linearidade óptica de terceira ordem (3) para baixas potências[18,19]. Além disso, o fato de ser um sistema com menor complexidade técnica comparado com sistemas de átomos frios, atraiu o interesse de pesquisadores para desenvolver sensores de última geração.
Magnetometria para diagnóstico médico
Entre as aplicações com grande potencial para os vapores atômicos está a magnetometria. A detecção de campos magnéticos tem ganhado recentemente muita atenção pelas suas aplicações em geofísica, navegação, medicina e indústria. Normalmente, os sensores Fluxgate são dispositivos bem estabelecidos que podem ser usados para medir campos com sensibilidade até nT. No entanto, medir campos magnéticos tão fracos como os emitidos pelos neurônios no cérebro, que são da ordem de pT-fT em uma escala de tempo de 0.001 segundos, não é uma tarefa simples. Até algum tempo atrás, os sensores SQUIDS (Superconducting Quantum Interference Device), uma bobina supercondutora sensível ao fluxo de campo magnético, foram o estado da arte para medir este tipo de campos magnéticos, possibilitando a realização de testes de Magnetoencefalografia (MEG) para diagnosticar doenças como epilepsia e esquizofrenia. Porém, o alto custo de operação desse tipo de sensor, devido ao sistema criogênico para manter as baixas temperaturas dos sensores, torna inviável a sua implementação em grande escala. No entanto, em 2002 o grupo de Romalis [20] mostrou o primeiro magnetômetro em vapores atômicos atingindo a sensitividade dos SQUIDs. Desde então, recentes trabalhos mostraram como é possível colocar magnetômetros atômicos em um capacete personalizado do paciente e estudar o teste MEG não apenas em adultos, mas também em crianças, ao contrário dos SQUIDs, que podem ter apenas um tamanho para adultos. Isto revolucionou a área, pois se projetou como uma alternativa sem custo de operação, alta taxa de amostragem, alta sensitividade e baixo custo de energia, como um novo tipo de sensor com potencial de grande escala.

Magnetometria na indústria e comunicações
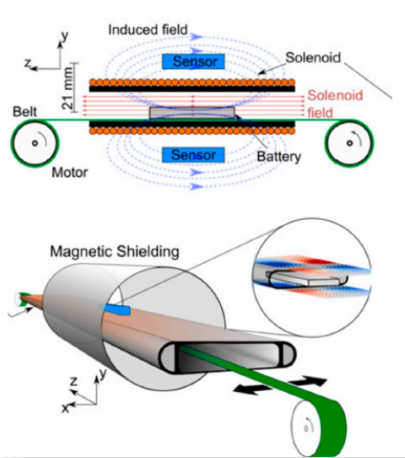
A partir desses trabalhos, tem-se mostrado aplicações em outras áreas. Por exemplo, na indústria é possível obter imagens magnéticas para detecção de objetos ocultos através de invólucros de metal, detecção não destrutiva de defeitos na fabricação de baterias de lítio e detecção de alvos subaquáticos. A tomografia de imagem é feita por indução magnética usando magnetômetro atômico. Na área de comunicação, tem-se usado magnetômetros atômicos para comunicação em cenários onde a comunicação por rádio apresenta desafios devido à atenuação ou interferência eletromagnética devido ao meio, como na comunicação subterrânea e subaquática no mar.
Magnetômetro atômico por Bombeamento Óptico
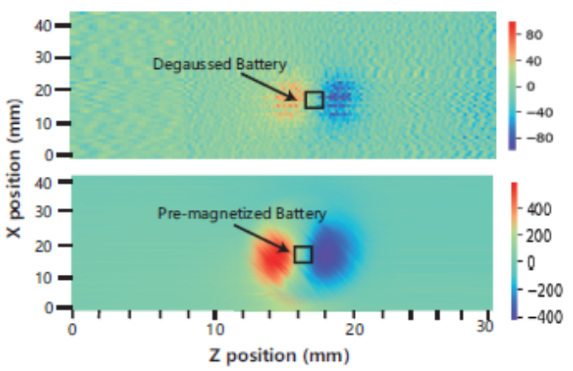
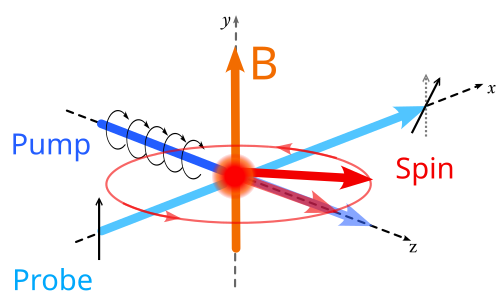
Magnetômetro Escalar – O princípio básico para magnetômetro atômico usa um feixe de luz polarizado circularmente que atua como bombeio ótico que produz polarização de spin de átomos, como é mostrado na figura 1. Na presença de campo magnético, o spin atômico precessa em torno do eixo do campo magnético. A precessão dos spins pode ser medida com a ajuda de um feixe de prova ortogonal que interage com a polarização linear. Ao medir a rotação de Faraday do feixe de prova, a birrefringência do meio é modulada com a frequência de Larmor dos spins, que pode ser medida por uma detecção balanceada.
A rotação de Faraday pode ser descrita pelo parâmetro de Stokes, de modo que para polarização linear com $S_x$ diferente de zero, a interação luz-matéria com amostra fina e sem efeitos de retro-alimentação é dada por: $$ \langle \hat S’_x (t) \rangle = \langle \hat S_x (t) \rangle – G_F ^{(1)} S_y n_F \langle \hat F_z (t) \rangle$$
onde o acento indica o campo de saída após interagir com o meio atômico, $\hat S_y = (c/2)(i \hat a^{\dagger}_{-} \hat a_{+} – i \hat a^{\dagger} _{+} \hat a_{-})$ representa o fluxo de fótons em luz polarizada num ângulo 45º expressa em termos de operadores de criação e aniquilação $\hat a_{\pm}$ e $\hat a^{\dagger} _{\pm}$ para componentes de polarização circular; $G^{(-1)} _F $ é a força de acoplamento de classificação k e $n_F$ é a densidade atômica com o mesmo estado hiperfino $F$.

Quando os átomos são preparados em estados polarizados de spin por um feixe de bombeamento, a polarização média é $\langle F_z \rangle \neq 0 $, produzindo assim uma rotação no feixe de prova polarizada linearmente. Na presença de campos magnéticos fracos, o spin interage com o campo magnético como $H_{int} = (\mu_B g_F/h) \vec{\hat F} \cdot \vec{B}$ produzindo a precessão da polarização geral $\langle F_z (t) \rangle \neq 0$, modulando assim o sinal de saída do feixe de sonda conforme mostrado pela eq.(1). Dessa forma, a luz do feixe de prova pode realizar a leitura da magnitude do campo magnético, e portanto, operar como um magnetômetro escalar.
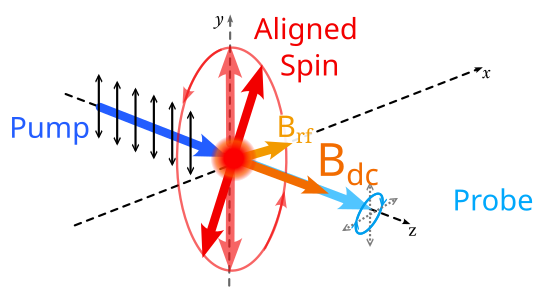
Magnetômetro vetorial – Ao invés de usar um bombeio com luz polarizada circularmente, é possível também usar um bombeiro com polarização linear para desenvolver um magnetômetro vetorial como o da nossa proposta na ref. [1]. O bombeio óptico prepara os átomos num estado de spin alinhado à direção de polarização do bombeio e perpendicular à direção de propagação, como é mostrado na figura 2. Ao vestir os estados atômicos por meio de radiofrequência, os spins conservam a precessão na presença de campo magnético estático que entra em ressonância com os estados atômicos. Para fazer a leitura dos spins atômicos, usamos efeito Voigt no feixe de prova para medir a elipticidade produzida pelos átomos. A rotação de Voigt para luz polarizada linearmente é devido à birrefringência linear induzida pela magnetização de um meio, neste caso os spins atômicos, alinhados no mesmo plano da polarização da luz. A interação luz-matéria para tal rotação é descrita pelo parâmetro de Stokes
$$ \langle \hat S’ _z (t) \rangle = \langle \hat S_z (t) \rangle + G^{(2)} _F S_y n_F \langle \hat F^2 _x (t) – \hat F^2 _y (t) \rangle $$
onde $S_z$ e $S_y$ representam as diferenças de fluxo de fótons em uma base de polarização circular e de 45º. Em termos dos parâmetros de Stokes, o efeito Voigt é uma rotação de polarização linear para elíptica na esfera de Stokes. O ângulo de rotação é proporcional a $ \langle \hat F^2 _i \rangle $, que é diferente de zero para estados alinhados, em vez de uma rotação de Faraday proporcional a $\langle F_z (t) \rangle $, que é diferente de zero para estados orientados. Esta é uma característica fundamental para ter uma operação de magnetômetro vetorial.

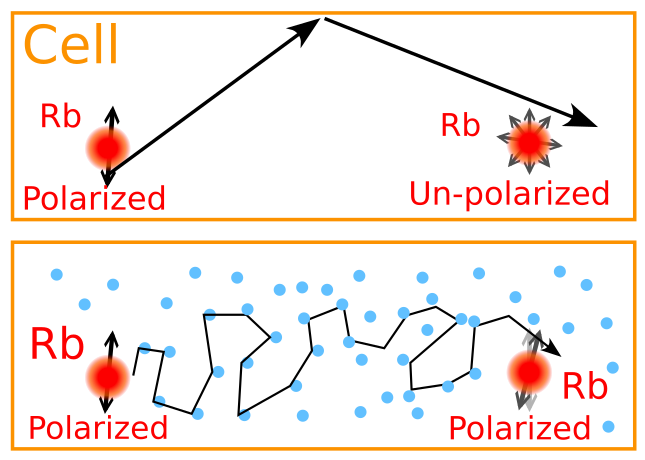
A célula de gas buffer usando espécies híbridas de átomos alcalinos, como na ref.[10], pode ser implementada para superar o relaxamento do spin e a depleção do feixe de bombeamento. Além disso, o projeto busca também implementar essa técnica de magnetômetro vetorial em células micro-fabricadas. O fato de empregar um feixe de bombeio com polarização linear, diferente do caso mais usado com polarização circular, permite que o feixe de prova seja acoplado de forma colinear ao bombeio, sem precisar usar uma configuração ortogonal como na maioria dos magnetômetro escalares. Empregar células de microfabricação, busca então, encaminhar o desenvolvimento deste tipo de sensores para escalas cada vez menores, e assim ganhar na optimização de fabricação de sensores.
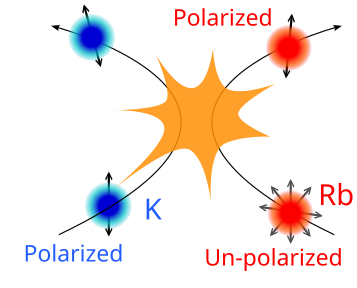
Interação com gases nobres – Recentemente tem se mostrado que o acoplamento de átomos alcalinos com gases nobres pode ser usado como co-magnetômetro em regime de acoplamento forte para aumentar a sensitividade dos magnetômetros. Os gases nobres não tem uma interação direta com luz no infravermelho e visível, isto faz com que os spins preservem a coerência dos estados por intervalos de tempo da ordem de horas. A leitura do estado de spin pode ser feita mediante a interação com átomos alcalinos, os quais podem ser lidos por luz infravermelha. Numa situação de acoplamento forte entre os átomos alcalinos e os gases nobres pode aumentar a sensitividades dos alcalinos na detecção de campos magnéticos. O projeto busca explorar essas propriedades para aumentar a sensitividade do magnetômetro vetorial.
[1] John Kitching, Appl. Phys. Rev. 5, 031302 (2018).
[2] Jonathon A. Sedlacek, Arne Schwettmann, Harald K¨ubler, Robert L¨ow, Tilman Pfau and James P. Shaffer, Nature Phys 8, 819–824 (2012).
[3] Christopher L. Holloway, Josh A. Gordon, Steven Jefferts, Andrew Schwarzkopf, David A. Anderson, Stephanie A. Miller, Nithiwadee Thaicharoen, and Georg Raithel, IEEE Transactions on Antennas and Propagation 62, 6169 (2014).
[4] Aishwarya Kumar et al. Nature volume 615, pages 614–619 (2023)
[5] Christopher G. Wade, Terahertz wave detection and imaging with a hot Rydberg vapour, Springer Theses, (2020).
[6] C. F. McCormick, V. Boyer, E. Arimondo, and P. D. Lett, Opt. Lett. 32, 178 (2007).
[7] B. J. Lawrie, P. D. Lett, A. M. Marino and R. C. Pooser, ACS Photonics 2019, 6, 1307 – 1318.
[8] C. F. McCormick, D. R. Solli, and R. Y. Chiao and J. M. Hickmann, J. Opt. Soc. Am. B 20, 2480-2483 (2003).
[9] Michelle O. Araujo, Hugo L. D. de S. Cavalcante, Marcos Ori´a, Martine Chevrollier, and Thierry Passerat de Silans, Phys. Rev. A 88, 063818 (2013).
[10] M.V. Romalis, Phys. Rev. Lett. 105 243001 (2010).
